Mexican Train strategy, or how to defeat the Grim Reaper

Much more than you wanted to know

Also in this series: Monte Carlo simulations of Crazy Eights/Uno, Love Letter, and Resistance/Avalon

If the Grim Reaper ever offers you a chance to play a game for your life, instead of going for a cliché like chess, I'd suggest challenging him to Mexican Train. Mexican Train has two beneficial properties in this situation:

1. If the Grim Reaper is unfamiliar with Mexican Train, your odds are excellent. An experienced player will easily dominate one without strategy, by as much as 2000:1 odds.

2. If the Grim Reaper is a Mexican Train expert, your odds are still good. Past a certain skill ceiling which is not difficult to achieve, the game is a toss-up, which could be the best you can hope for anyway.

Chess has the first property but not the second, the skill ceiling for chess may exceed what's possible with the computational resources of our universe. A number of games from War to Candyland have the second property but not the first, as there’s no edge for an experienced player.

So, you may be asking, what is this game which could improve my odds against the dread ferryman of souls?

I don’t recommend this game, it’s rigged

Mexican Train is a dominos variant, so get ready to break out your colored tiles. Players are dealt a hand of dominos, then take turns playing dominos/tiles until someone has played their entire hand, at which point the other players add up all remaining points in their hand (the ideal score is zero). Players can play tiles matching the last pip on their own train, on a public train known as the Mexican Train, or any train which has opened due to that player being unable to play.

My wife has strong feelings about the aesthetic elegance this game is capable of, which this image does not live up to. Proper domino placement deserves its own blog post

You can read more about the rules here, or pick up a copy here. What makes the strategy interesting is that players have to plan ahead; because you can always play on your own train, to improve the odds you can use up your own tiles you can plan out a continuous path with your tiles, matching pips for as long as you can. If you started by playing a 12:5 in the picture above, you should have a plan to play a domino that starts with a 5 next, then a domino that matches whatever is opposite the five, and so on for as long as you can given the tiles you were dealt.

Peak popularity for this game occurs at December every year, suggesting people mostly play this game with their families over Christmas

To analyze the strategy of this game, I wrote a Monte Carlo simulation, where I coded up the rules of the game, pitted AIs using different strategies against each other in a tournament, then compared their average scores and win-rates. The following strategies showed meaningful divergence:

Random. Play a random legal move.

Greedy. Play the largest domino you can.

RandomPath: Build a path by randomly selecting an eligible tile which continues your current path, and repeat that process until you can no longer extend your path.

When playing, preferentially try to offload doubles and tiles that are not part of your path.

LongestPath: Evaluate all possible paths you can generate with your current tiles, and select the longest path, tiebreaking on the path with the largest sum.

When playing, preferentially try to offload doubles and tiles that are not part of your path.

The following table shows how effective the strategies are when pitted against each other. The first number shows the average score of the players using the strategy on that row (remember, low numbers are good), and the second number shows the average winrate for that strategy (for example, a strategy gets 50% playing against itself).

These samples are taken from a 4 player game where two AIs of each type compete, across a full round where each of the 13 doubles is used as the starting tiles. The game is repeated thousands of times to see which strategies win more often.

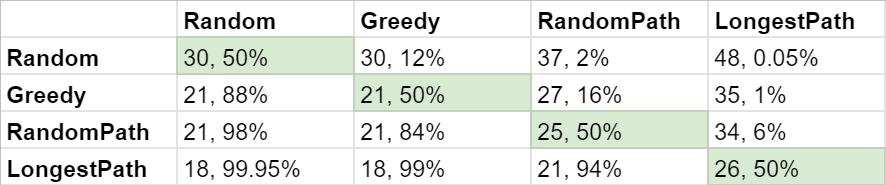
As an example from the above table, the second cell in the first row [30, 12%] shows that Random Players have an average score of 30 against Greedy Players and win 12% of the time. The equivalent cell on the second row [21, 88] shows that Greedy Players have an average score of 21 against Random Players and win 88% of the time.

Some observations:

• Each level of strategy crushes the next weakest one. Greedy Players win 88% of the time against Random Players, RandomPath Players win 84% of the time against Greedy Players, LongestPath players win 94% of the time against RandomPath Players.
  
  On that last point, I was surprised by the extent to which an optimal pathing algorithm dominates a pathing algorithm that short-circuits after a randomly found path; the quality of your path matters.

• The algorithm which best minimizes individual scores doesn’t minimize group score, akin to the prisoner’s dilemma. When all players are using the Greedy strategy, average scores are lowest. When all players are using the LongestPath strategy that gives them the highest winrate, average scores increase relative to every strategy other than Random. The strategy which yields the best individual scores does not yield the best scores for the group, because it’s designed to go out fast and leave other players with high scores.

LongestPath, your ticket to victory

So, LongestPath absolutely crushes a number of basic strategies, including naïve path-building. How difficult is to implement for human players? In principle, the longest-path problem is believed to be exponentially difficult; no easier algorithm than brute-forcing possibilities is known to exist, unless the founding principles of cryptography are wrong.

That said, there are only so many possibilities to brute force, given the limited number of dominos and ways they can connect. Consider the following set of 23 dominos, which came up in a game the computer played against itself. What's the longest continuous train you can build, starting with a three?

7:6 9:2 10:10 7:2 10:3 8:3 7:4 10:6 3:1 4:2 8:1 9:8 7:3 5:4 9:3 2:1 10:7 11:0 8:5 6:6 3:2 5:0 9:5. Must start with a 3.

The naïve algorithm I wrote searched over a million possibilities to find the optimal train through these dominos. (if you want to know the length of that optimal sequence, check the end of the post; knowing the optimal length makes the problem easier, because you know when to stop looking). If you want to give it a shot, get out your dominos, and try to make the most efficient path you can. My wife and I did the same, and managed to find an optimal path without too much trouble. Given that this is feasible for humans, I suspect there are basic heuristics which substantially reduce the complexity, but it’s still a small enough problem for a computer to brute force and run multiple games at high speed.

Give that set of dominos above a try, if you haven’t yet. If you can crack that sequence, which is at the tail end of complexity you’d normally encounter, I think you can handle anything the grim reaper can throw at you.

---

Appendix A, the longest path algorithm in more depth

1. Construct the longest train you can. Refresh this if your play is ever disrupted by a double or being forced to draw.

2. If you are forced to make a move by a double, try to play a tile which does not disrupt your train. If you must play a tile which does disrupt your train, pick the one which leaves the longest train in place.

3. Otherwise, if you have a double you can cleanly play on another track or as the last tile on your track, play it, then play again.

4. Otherwise, if your train is open, play on it to close it.

5. Otherwise, if you have an available move which is not part of your planned train, play the largest such domino

6. Otherwise, if you can play on your own train, play it.

Areas that could take more optimization, but which I suspect to have diminishing returns:

1. Unloading points over maintaining a train. Experimentation suggest that optimizing for train length beats optimizing for score. An algorithm targeting the train with the LongestPath consistently outperforms an algorithm targeting the train with the LargestScore, where longest path wins 51.3% of the time.
   
   That said, there may be edge cases where you are far enough behind or your opponents are close enough to going out that it makes sense to break some of the above rules to unload points quickly, but I would expect the margin to be small

2. Targeting dominant players. Other than optimizing for your own score, there are situations where one player is ahead in the point total for the game, and optimizing around not helping that player’s train, and only playing tiles that player does not benefit from, may outweigh the benefits of optimizing for your own chances of winning that round

3. Tile-counting. There may be scenarios where tracking which dominos have been played may allow you to minimize the chances other players can play on public trains, harming other players at your own benefit.

If anyone has strong intuitions around how much any of those strategies would help or hurt an algorithm, I’d be interested to hear them, or explore them in a follow-up post. I would guess that given that optimizing for train length versus size doesn’t significantly affect results, that the swing in odds would be nowhere near as large as other strategies.

Appendix B, the longest train against the sequence above

Why are so many Turians Catholic? Because they believe in Mass Effects. This joke has a search depth of three.

Is 20 tiles long. Let me know if you find it